Research activities

Extracting the hidden structure of glass

Understanding the behaviour of glass is a long-standing mystery in materials science. On large scales, glass is rigid and behaves like a solid. But curiously, its microscopic structure is disordered and looks like a liquid. Because of this, it is difficult to predict its mechanical properties with theory, which means that new advanced glasses can only be designed through trial and error. How can we understand the structure of glass in a way that’s useful for predicting its behaviour?

One possible solution is to classify a material’s structure by how much the atoms vibrate, which could be measured by looking at how much the material’s diffraction pattern has been “blurred”. This is done routinely for crystals. I am investigating how this can be done for amorphous materials. The outcome will be a measure of structure based on how constrained each particle is. Using this new measure of structure, I aim to link the microscopic structure of glass to its macroscopic properties via computer simulations. This should give us an improved understanding of the nature of glass, and provide significant benefits, such as an increased ability to rationally design amorphous materials with desired properties.

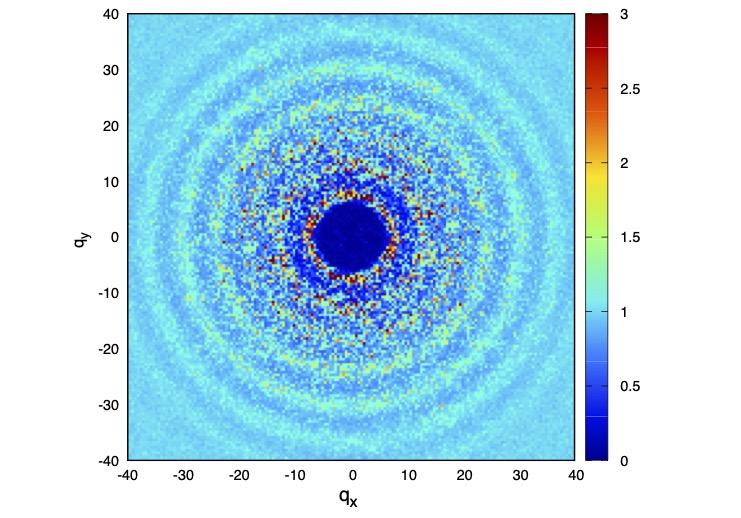
Constrained liquids and glasses

Liquids confined to small spaces display complex behaviour. One key feature is that the density of the liquid is not uniform, but varies with distance from the confining walls. A remarkable property of these liquids is that the degree of ordering among the particles changes non-monotonically with the degree of confinement. Likewise, the glass transition also shows a non-monotonic dependence on confinement length. My research seeks to disentangle the intrinsic effects of confinement from the byproduct of the non-uniform density profile.

The first approach is to study a quasi-confined liquid, where the liquid is confined to the surface of a (4D) torus. In this homogenous system, the density is uniform, allowing us to investigate the intrinsic effects of confinement.

The second approach is to study a liquid which is not confined, but instead has a field applied to the particles to impose a modulated density artificially. Complementary to the torus approach, this allows us to investigate the effect of density modulation independently of confinement. The goal of this work is to characterize the glass transition in the modulated liquid, and compare it to that in confined liquids.
Journal of Statistical Mechanics: Theory and Experiment, 8, 083216 (2019)

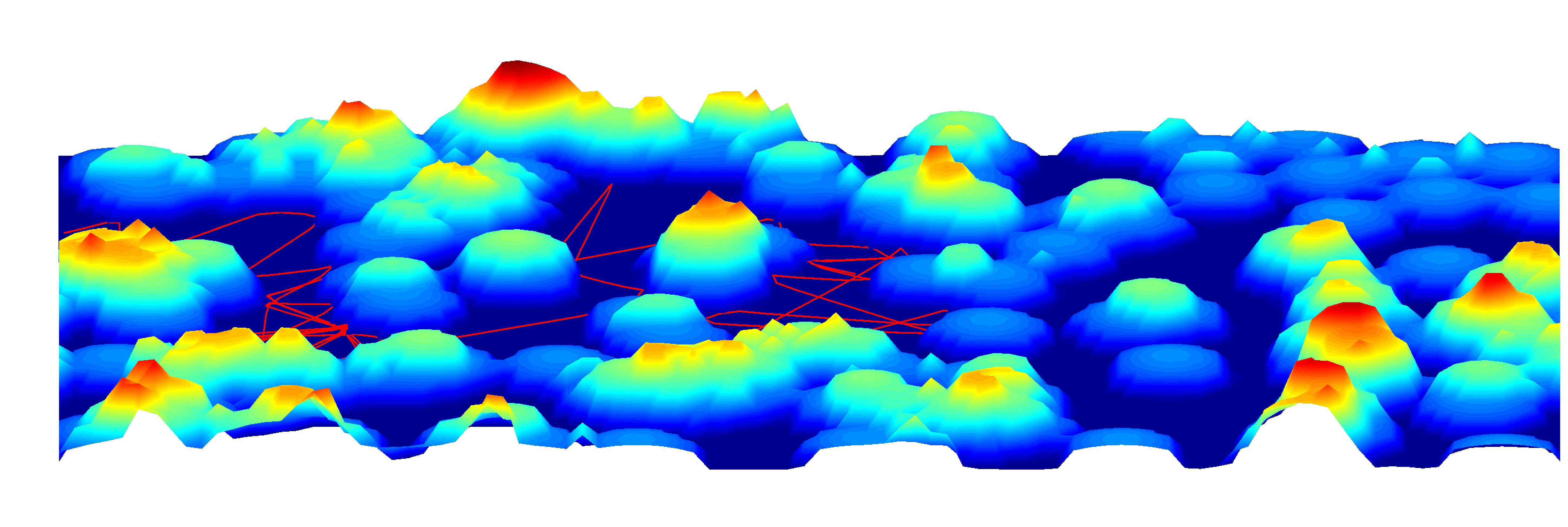
Transport through porous media

Liquids in crowded environments occur in many situations, including inside of cells, in catalysts, and in porous rock during oil recovery. Both experimentally, and in simple models, the transport in complex crowded media can be subdiffusive. The origin of this anomalous diffusion has been explained theoretically for the simple Lorentz model. I extend the Lorentz model towards realistic systems by relaxing one assumption of the model (the hard-exclusion interaction), and find that they system exhibits a percolation transition dependent on the energy of the probe particle, and the dynamics remain subdiffusive at the percolation point.
Soft Matter, 15, 3906 (2019)

Experimentally realisable spin models

Simple models are used extensively by physicists to probe the underlying physical processes of real systems. Ising type models, which consist of a number of interacting spins each with one degree of freedom, are particularly popular. Recent advances in lithography of nanomagnets has allowed such toy models to be built and imaged experimentally. In collaboration with experimentalists, I study how the geometry of the lattice can be tuned to allow us to investigate interesting physical effects like charge screening and frustration.
Science Advances, 5 (2), eaav6380, (2019)
Appl. Phys. Lett. 112, 092403 (2018)
Nature Communications 8, 995 (2017)
Nature Communications 7, 12635 (2016)

Disordered metamaterials

Metamaterials are characterized by the property that their function is determined by their geometry, rather than their composition. One example of these, called “auxetic”, have the counter-intuitive behaviour of expanding laterally when stretched longitudinally. Porous solids, such as polymer or metallic foams, are examples of man made auxetic materials. These architected materials are designed with a re-entrant cell structure. Simple two dimensional models with re-entrant geometries have successfully reproduced this auxetic behaviour. We investigate the effect of disorder in these simple structures, and how it influences the auxetic properties.
Eur. Phys. J. B 91: 271. (2018)

The Fluctuation Theorem in non-equilibrium statistical mechanics

In microscopic systems, there is a finite probability that the second law of thermodynamics will be violated on short time scales. This is quantified by the fluctuation theorem, in terms of a quantity called the dissipation function. In my PhD research, I investigated the significance and statistics of this function in the fluctuation theorem and related results, as well as used it to probe non-monotonic relaxation towards equilibrium.
J. Chem. Phys. 144, 074107 (2016)
Mol. Simulat. 42, 531 (2014)
Commun. Theor. Phys. 62, 476 (2014)
J. Chem. Phys. 139, 184106 (2013)
Thesis: An Investigation Into the Significance of Dissipation in Statistical Mechanics